|
|
商学院 |
|
| 三角形的正弦(sine)、余弦(cos)、正切(tan) |
 |
|
| 《初中汉语语法精要》作者 |
| 查看专辑《有趣的数学》的全部文章 |
 |
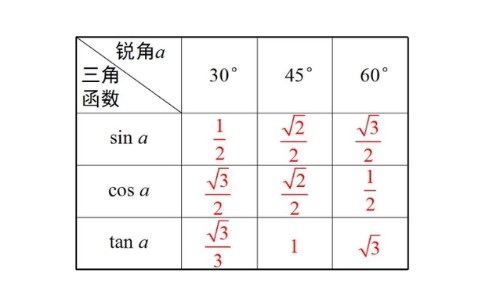
正弦(sine) 数学术语,是三角函数的一种,在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边。 正弦函数 一般的,在直角坐标系中,给定单位圆,对任意角α,使角α的顶点与原点重合,始边与x轴非负半轴重合,终边与单位圆交于点P(u,v),那么点P的纵坐标v叫做角α的正弦函数,记作v=sinα。通常,我们用x表示自变量,即x表示角的大小,用y表示函数值,这样我们就定义了任意角的三角函数y=sin x,它的定义域为全体实数,值域为[-1,1]。 正弦定理公式 a/sinA=b/sinB=c/sinC=2R。 【注1】其中“R”为三角形△ABC外接圆半径。下同。 【注2】正弦定理适用于所有三角形。初中数学中,三角形内角的正弦值等于“对比斜”仅适用于直角三角形。 正弦定理推论公式 1、(1)a=2RsinA; (2)b=2RsinB; (3)c=2RsinC。 2、(1)a:b=sinA:sinB; (2)a:c=sinA:sinC; (3)b:c=sinB:sinC; (4)a:b:c=sinA:sinB:sinC。 【注】多用于“边”、“角”间的互化。 3、由“a/sinA=b/sinB=c/sinC=2R”可得: (1)(a+b)/(sinA+sinB)=2R; (2)(a+c)/(sinA+sinC)=2R; (3)(b+c)/(sinB+sinC)=2R; (4)(a+b+c)/(sinA+sinB+sinC)=2R。 4、三角形ABC中,常用到的几个等价不等式。 (1)“a>b”、“A>B”、“sinA>sinB”,三者间两两等价。 (2)“a+b>c”等价于“sinA+sinB>sinC”。 (3)“a+c>b”等价于“sinA+sinC>sinB”。 (4)“b+c>a”等价于“sinB+sinC>sinA”。 5、三角形△ABC的面积S=(abc)/4R。其中“R”为三角形△ABC的外接圆半径。 表达式:f(x)=Asin(ωx+φ) 余弦(cos) 数学术语,是三角函数的一种,在Rt△ABC(直角三角形)中,∠C=90°,∠A的余弦是它的邻边比三角形的斜边,即cosA=b/c,也可写为cosa=AC/AB。 余弦函数:f(x)=cosx(x∈R) 余弦定理:三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。 余弦定理公式 (1)a^2=b^2+c^2-2bccosA; (2)b^2=a^2+c^2-2accosB; (3)c^2=a^2+b^2-2abcosC。 【注】余弦定理及其推论适用于所有三角形。初中数学,三角形内角的余弦值等于“邻比斜”仅适用于直角三角形。 余弦定理推论公式 1、cosA=(b^2+c^2-a^2)/2bc; 2、cosB=(a^2+c^2-b^2)/2ac; 3、cosC=(a^2+b^2-c^2)/2ab。 三角形的正弦定理和余弦定理公式及其推论常用来解三角形。对于某些复杂题,需要把正弦定理和余弦定理及其推论综合起来运用。 【例题】已知三角形△ABC中,角A=30°,a=2,求三角形△ABC外接圆的面积。 解:设三角形ABC外接圆半径为R, 根据正弦定理得:a/sinA=2R, 所以R=a/(2sinA)=2, 所以,三角形ABC的外接圆面积S=4π。 正切(tan) 数学术语,在Rt△ABC(直角三角形)中,∠C=90°,AB是∠C的对边c,BC是∠A的对边a,AC是∠B的对边b,正切函数就是tanB=b/a,即tanB=AC/BC。 即:在Rt△ABC中,如果锐角A确定,那么角A的对边与邻边的比值随之确定,这个比叫做角A的正切,记作tanA。 即:tanA=∠A的对边/∠A的邻边。 正切定理: (a + b) / (a - b) = tan((α+β)/2) / tan((α-β)/2) |
 |
|
声明:该文及以下回复观点仅代表作者本人,五略商书系信息发布平台,仅提供信息存储空间服务。
转载请注明作者和出处:转自《五略商书》,作者董荣天! |
|
| 相关阅读 |
|
孩子,请你快乐地飞翔
|
|
|
孩子,请你自由地飞翔
|
|
|
父母课堂读后感
|
|
|
孩子,我想对你说
|
|
|
陪伴成长
|
 |