|
|
商学院 |
|
| 【第9章】 QC七大手法之——直方图 |
 |
|
| 精益管理咨询师,五略管理法创始人 |
| 查看专辑《QC(质量管理)管理工具及七大手法》的全部文章 |
 |
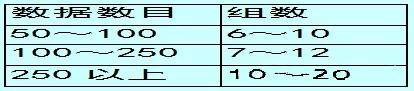
定义: 将所收集的数据、特性值或结果值,在横轴上适当地区分成几个相等区间,并将各区间内测定值所出现的次数累加起来,用柱形画出的图形。 使用目的: 1.测知制程能力。 2.测知数据的真伪。 3.测知分配型态。 4.计算产品不良率。 5.调查是否混入两个以上的不同群体。 6.藉以制定规格界限。 7.规格与标准值比较。 8.设计管制界限是否可用于制程管制。 9.求分配的平均值与标准差。 制作步骤: 1.收集数据并且记录在纸上。 2.找出全体数据中之最大值(L)与最小值(S) 3.定全距(R)=最大值(L)-最小值(S) 4. 决定组数 ——史特吉斯公式组数:K=1+3.32log n n=数据个数 ——组数决定参考表(经验法则)
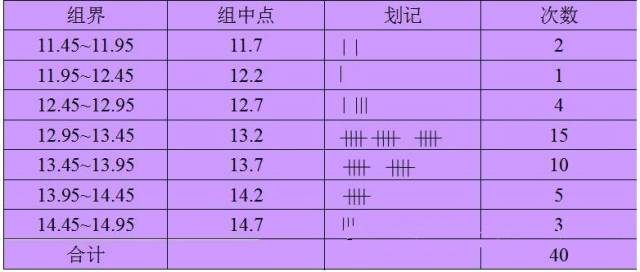
5. 定组距(H)=R/K=全距/组数 6. 求各组上、下组界 ——第一组下组界=最小值-最小测定值/2 ——第一组上组界=下组界+组距 (以此类推) 7. 决定组的中心点。 ——(上组界+下组界)/2=组的中心点 8. 制作次数分配表。 9. 制作直方图。 10. 填上主题、规格、平均值、数据来源、日期等数据。 次数分配表:
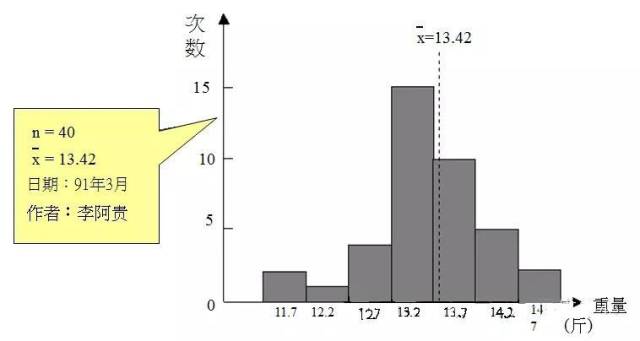
范例:西瓜重量直方图
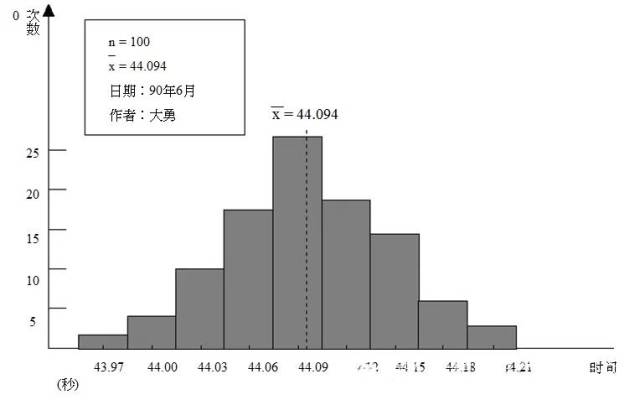
范例:小勇跑步所需时间直方图
注意事项:
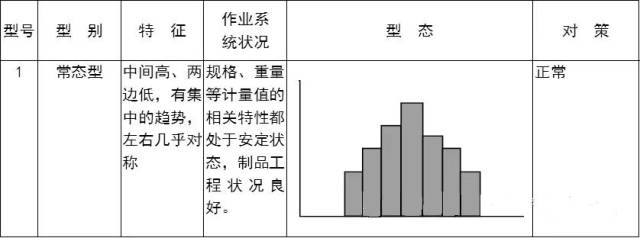
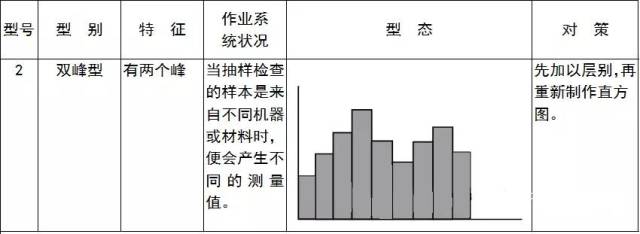
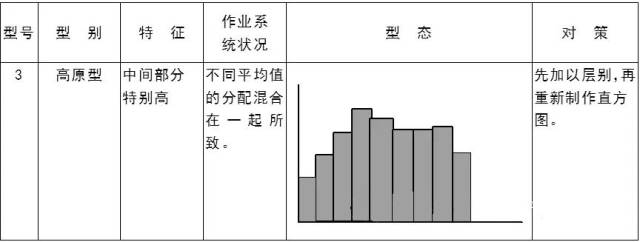
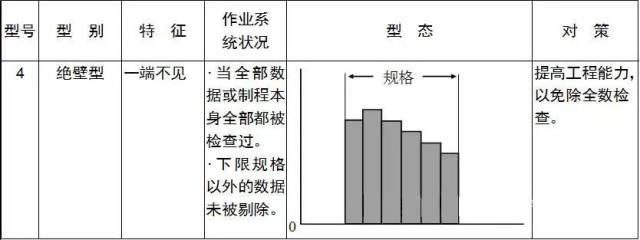
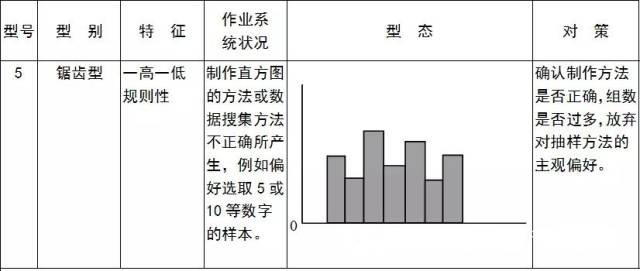
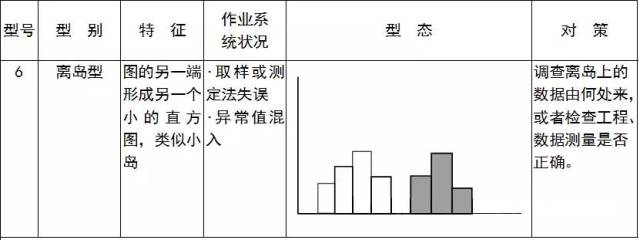
型态、形成原因与对策:
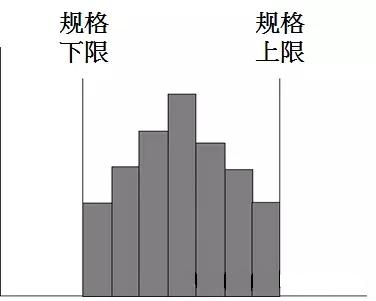
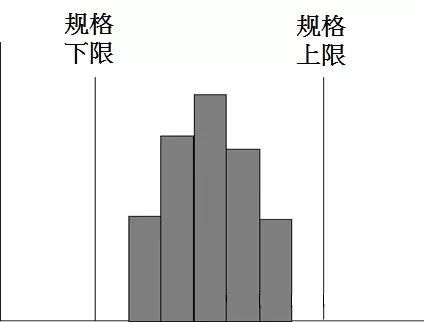
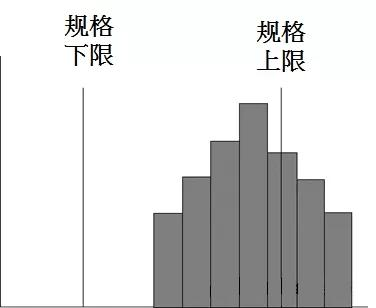
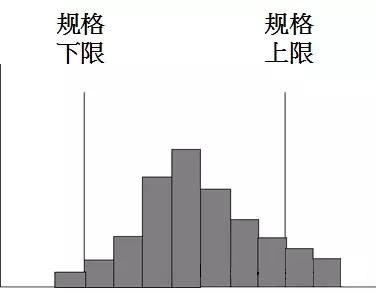
分布型态与目标规格比较: 1.图形是否分布中央? 2.规格外比率有多少? 3.平均值是否在规格正中央?
制程能力还可以,但产品质量稍有变动即会产生不良品,有提高制程能力的必要。
制程能力足够,产品质量分散宽度完全在规格界限内。
制程能力不足,因为中心值偏右,如能将中心值调整至规格中心处,则刚好可以符合规格。
——制程的分散宽度过大,此时须改善制程或检讨规格,而已生产的产品须全选别。 |
|
声明:该文及以下回复观点仅代表作者本人,五略商书系信息发布平台,仅提供信息存储空间服务。
转载请注明作者和出处:转自《五略商书》,作者董立杰! |
|
| 相关阅读 |
 |