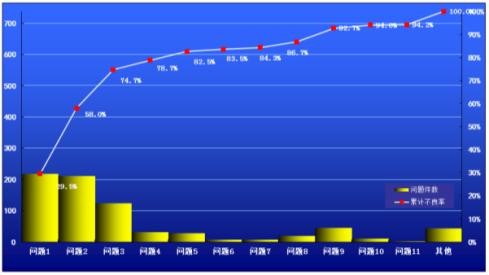
（1） 定义

柏拉图是在分析问题后，在得出的大量问题中如何确定出主要问题的一种重要的分析工具。柏拉图常被用在完成鱼骨图分析及资料搜集后，通过对问题发生现象的数据统计、归类、分析，使用次数分布技术，区分出“少数重点因素”和“大量微细因素”，将少数的影响结果的因素确定出来以最少的代价解决掉最多的影响。

（2） 如何使用

第一、统计数据，并按照问题的因素影响程度将数据按照降序排列，如下图所示：

第二、计算因素造成的问题的累计占比数，如上图“累计不合格率”，其中因素1的累计不合格率等于其不合格率；因素2的累计不合格率等于因素1不合格率加因素2的不合格率，以此类推，直到累计100%为止。如上表所示；

第三、按照表做出如下图所示的图表。其中图表中X坐标为问题的各个因素，纵坐标主轴为问题因素发生的数量，次坐标则为问题因素发生的累积百分率；

第四、在图表中选出累计百分比达到80%左右的所有问题因素。其中占比80%的因素可以在80%左右偏差，不做严格的规定。则，确定的达到累计为80%的几个因素则为影响问题发生的主要因素；

第五、根据确定的主要因素制定改善对策并加以跟踪；